为抑制空间柔性桁架结构的低频振动，采用压电杆件进行优化配置实现桁架结构的振动主动控制；建立了空间桁架结构主动压电杆件的机电耦合模型，利用ANSYS前处理功能编制了压电桁架的机电耦合有限元程序；将可控性度量指标与逐步消减法相结合，实现了空间桁架结构主动杆件的优化配置；对结构进行初始位移扰动、正弦激励以及随机激励，并采用最优模态控制算法进行振动抑制仿真分析，对上述方法进行验证且建立振动控制评价指标进行评价；结果表明将可控性度量指标与逐步消减法相结合的方法可有效抑制空间柔性桁架结构的振动。
关键词：空间桁架；振动控制；优化配置；模态控制
0 引言
近年来，大型化、低刚度、柔性化是各卫星天线结构发展的重要趋势，然而该类柔性结构具有模态阻尼小等特性，当在太空运行受到外界激励时，若不采取措施对其振动进行抑制，则振动将会持续很久，造成定向精度、姿态稳定等问题，严重时可能导致结构受到破坏，降低结构使用寿命[1-2]。
由于压电陶瓷材料具有刚度高、频带宽、高转换率、质量轻等特点，在桁架结构中常被用于制作传感器和作动器。郑凯等人设计了采用压电堆作动器的压电主动构件[3]；曹玉岩等人根据有限元理论和Hamilton原理建立了平面智能桁架结构动力学模型，并根据线性二次型最优控制理论建立了最优振动控制模型[4]；陈文英等人基于Lyapunov综合法设计了一种稳定的直接型自适应模糊主动振动控制器并在一平面16杆智能桁架结构进行了仿真验证[5]；Marinaki 等人研究了应用PSO 算法优化的模糊控制器进行梁的振动控制[6]；Sun 研究了挠性航天器的模糊预测振动[7]；Zhu 等人研究了采用滑模模糊进行挠性航天器的振动和姿态机动控制[8]；所有这些研究都取得了较好的控制结果，然而关于空间桁架结构振动的研究很少；Armaghan等人建立了桁架结构三维梁模型[9]；李东旭等人采用遗传算法得到了作动器和传感器在大型智能桁架系统中的最优位置并利用T字型桁架结构进行了验证性试验，然而遗传算法中各参数需主观确定且计算速度较慢[10]。
针对作动器、传感器位置优化问题，目前已经提出了多种作动器传感器优化配置准则，主要有可控度可观测准则、系统能量准则、系统响应准则、可靠性准则、控制溢出观测溢出准则等。可控度准则具有明确的物理意义，不需要与控制算法联立，求解简单有效，获得广泛的应用。刘福强[11]利用逐步消减法对作动器传感器配置做了优化，提高了求解效率，Sylvaine L从基于能量的角度出发，给出了3种不同的准则来配置作动器输入能量最小准则、结构总能量最小准则，可控性格兰姆矩阵特征值最大准则，并且指出，在阻尼较小的情况下，它们是等价的，并给出了可控度综合指标[12]。
本文以空间柔性桁架结构为研究对象，首先建立了空间桁架结构主动压电杆件的机电耦合模型，并利用ANSYS、Matlab编制了空间桁架结构动力学分析程序；其次将综合可控度指标与逐步消减法结合实现主动压电杆件的优化配置；最后采用最优模态控制算法进行了空间桁架结构的控制仿真验证，并进行振动控制效果评价。
1 空间桁架动力学模型
1.1 压电杆件作动理论
桁架结构主动杆件采用多层式压电陶瓷驱动器，如图1所示，φ为压电薄片两端电势差，t为压电薄片厚度，L为压电杆件长度，N1、N2分别为杆件两端轴向力。
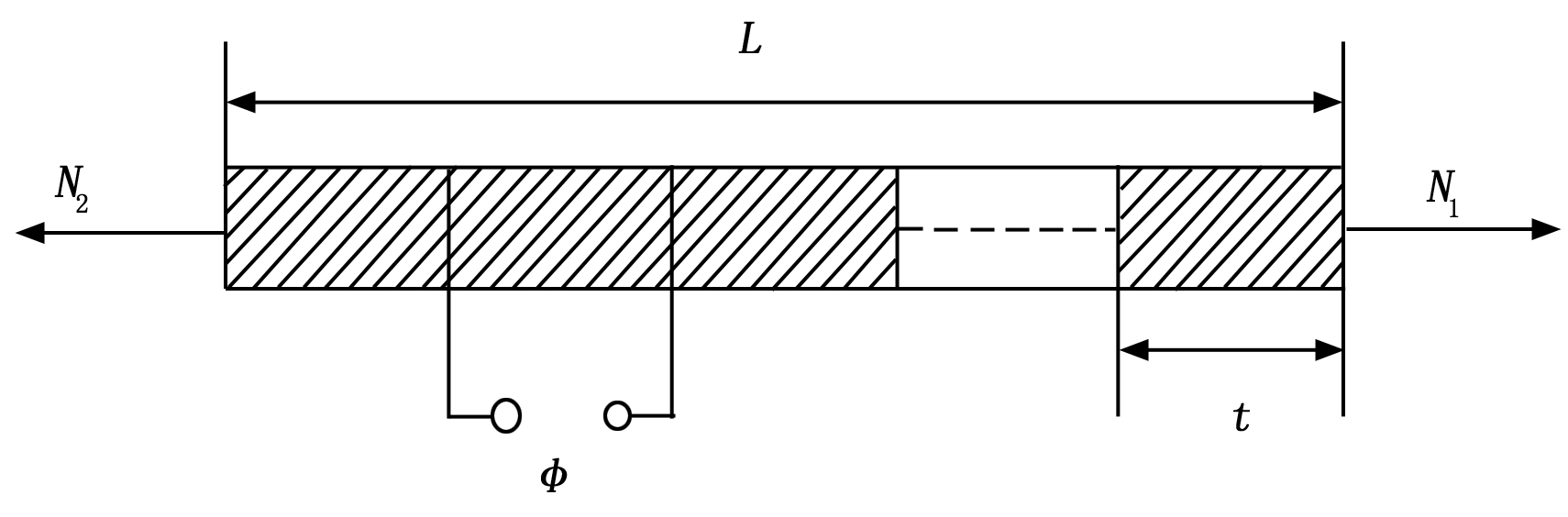
图1 压电杆件
若只考虑杆轴方向的压电效应，图1所示压电杆件的力平衡方程和电荷平衡方程为
(1)
其中:e33为轴向压电系数，c33为轴向弹性系数，ε33为轴向介电系数。
每个压电薄片均可视为平行板电容器，若没有泄漏电流，电荷量{Q}与施加于压电薄片外电压{V}之间关系为
(2)
其中
2，ci为第i根压电杆的等效电容参数，Ai为第i根压电杆截面积，m为压电杆件总数。
采用有限元方法[14]，对公式(2)进行坐标转换，用Guran方法消去电势差，得到压电作动器的有限元动力学方程为
(3)
压电单元端部需要连接普通杆件或预压弹簧，此时压电主动杆件需考虑耦合刚度项和电荷载向量，力平衡方程如式(4)所示：
(4)
其中:Δ=k1k2+k1k3+k3k2，k1,k3为连接压电单元两端的杆件或弹簧刚度，k2为压电单元的刚度，
。
1.2 空间桁架结构模型及动力学分析
本文研究的空间桁架简化结构如图2所示，该结构共由12个正六面体柔性桁架单元组成，共52个单元，161根杆件。桁架单元如图3所示，每个单元均由空心球体、弹簧和空心杆组成，共8个节点、18根空心杆，其中包括12个边长杆及6个对角杆。空心球体和空心杆材料均为不锈钢。所有节点均为弹性平移铰，节点内部连接情况如图4所示。
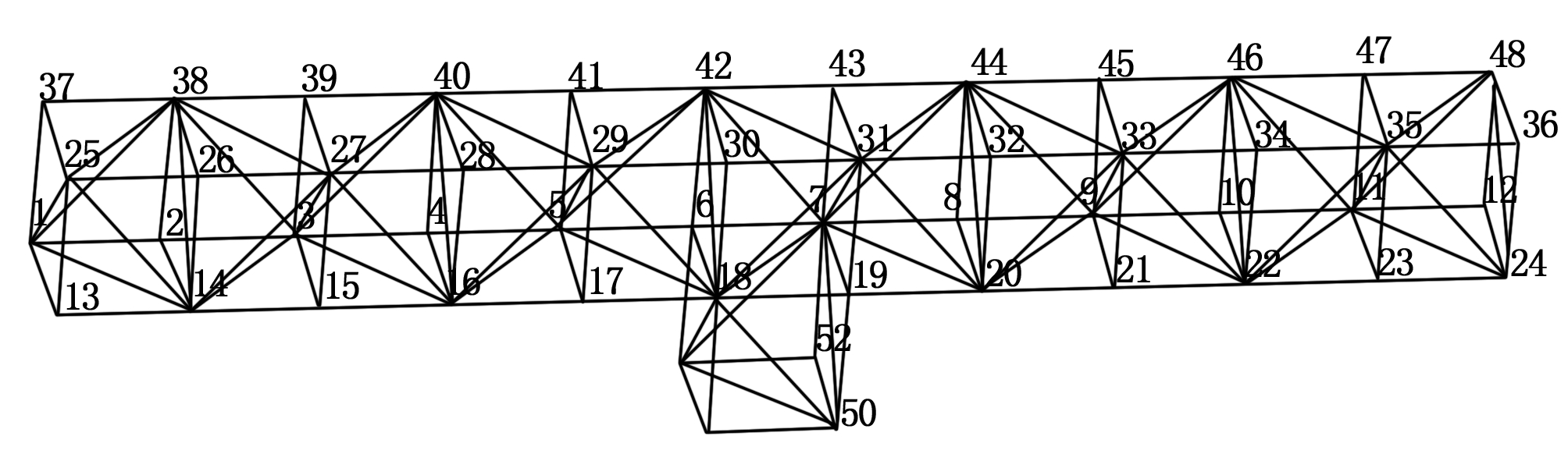
图2 空间桁架结构
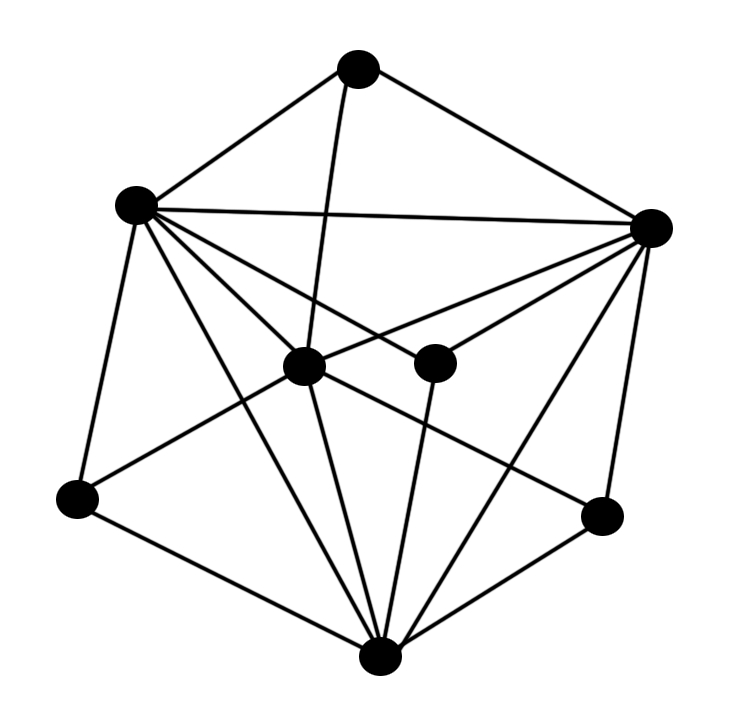
图3 桁架单元模型
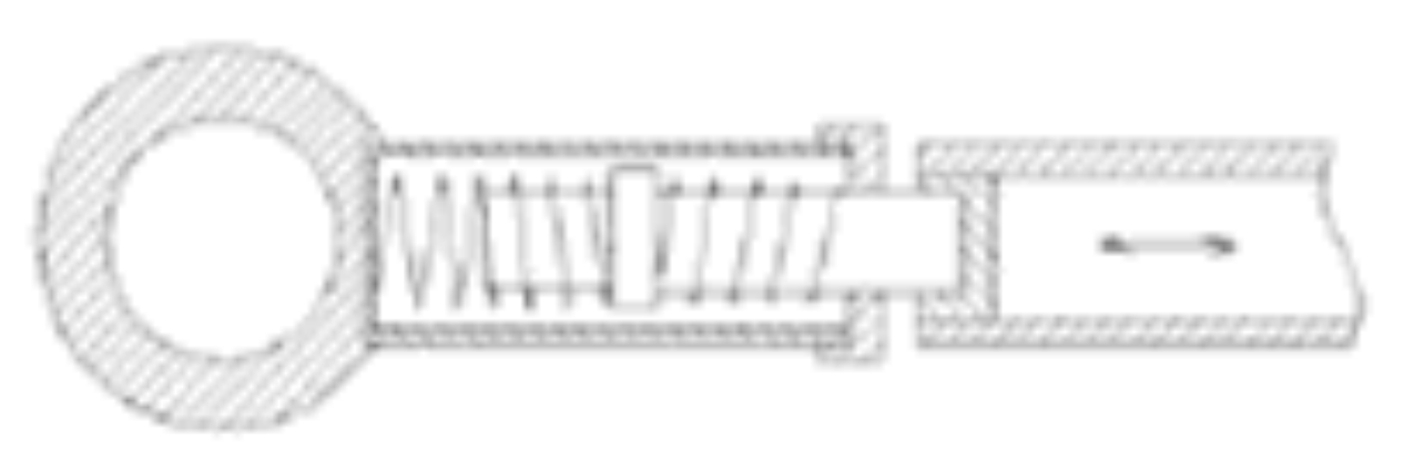
图4 桁架节点内部结构
由于杆件节点较多，先利用ANSYS命令流生成桁架结构有限元模型，利用APDL语言编写提取出单元编号及对应节点编号和位置信息储存到数组，将数组导入MATALAB编写程序。
杆端弹簧按照与杆件串联处理，凸出的六面体认为固定在航天器上，空心球按集中质量处理，对结构进行模态分析，分析结果如表1所示。
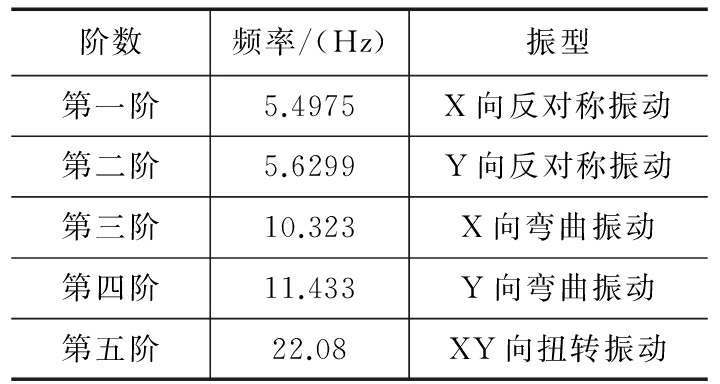
表1 空间桁架模态分析结果
阶数频率/(Hz)振型第一阶5.4975X向反对称振动第二阶5.6299Y向反对称振动第三阶10.323X向弯曲振动第四阶11.433Y向弯曲振动第五阶22.08XY向扭转振动
结果表明，前5阶模态主要为X及Y方向的振动，因此在对结构桁架进行振动控制时主要对X方向及Y方向进行控制。
2 主动杆件优化配置
随着大型航天结构控制技术的发展，主动杆件的位置优化是一个重要问题。通过主动杆件位置的选择，可改善控制器的性能。合适的优化位置不但影响控制效果，且影响控制系统能量的消耗。本文基于可控性度量指标和逐步消减法进行主动杆件的优化配置。
将式(3)表达为状态方程形式，离散化后如式(5)所示：
(5)
记
，其中nc为控制模态数目。
系统的可控性格兰姆矩阵Wc如式(6)所示：
(6)
定义作动器系统的可控性度量指标如式(7)所示[12,13]：
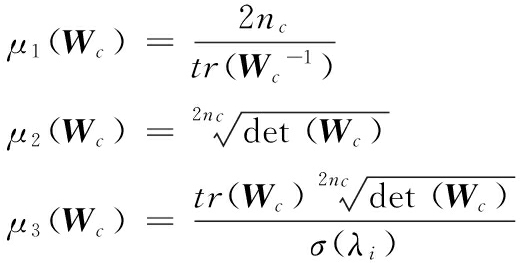
(7)
指标值越大，系统可控度越高。逐步消减法[12]是从剩余的作动器的候选位置中去掉一个对目标函数贡献小的候选位置，直至目标数目的候选位置，当s个可选位置上配置有作动器时，矩阵Pc的维数为2ncs×2nc，则式(6)表达如下
(8)
pi为矩阵Pc的第i行数据。删除一个作动器的可选位置时有：
(9)
pj为Pc中与这个作动器可选位置相关联的2nc行数据。
优化μ1，μ2，μ3过程中，删除μ1(Wcs-1)，μ2(Wcs-1)，μ3(Wcs-1)最大值相应位置的杆件，以保证剩余杆件的配置可控度最大。逐步消减法主动杆件优化配置结果如表2所示。
表2 逐步消减法主动杆件优化配置
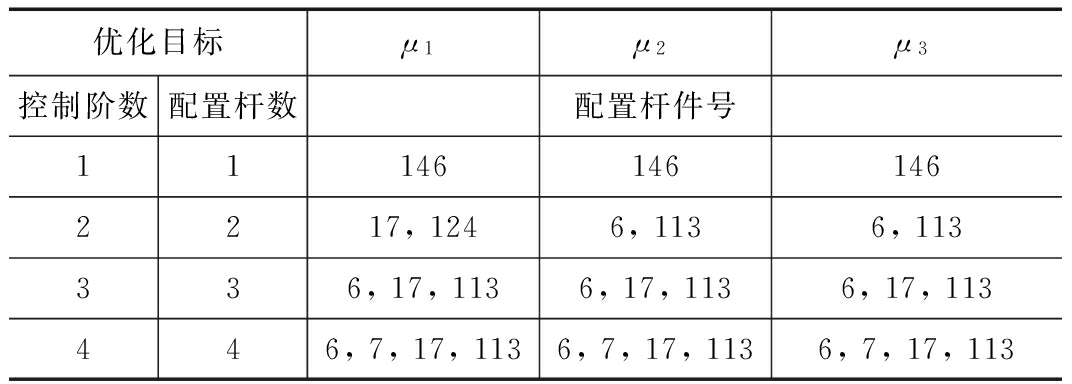
优化目标μ1μ2μ3控制阶数配置杆数配置杆件号111461461462217,1246,1136,113336,17,1136,17,1136,17,113446,7,17,1136,7,17,1136,7,17,113
结果表明3种指标的优化结果接近，在控制第二阶模态时杆件配置略有差别且高阶模态配置时基本包括了低阶模态配置的杆件。
3 控制仿真与分析
为验证主动杆件优化配置的有效性，对上述模型在主动杆件优化配置及主动杆件选配位置两种情况进行振动控制仿真计算。对式(3)进行模态坐标转换，结果如下：
(10)
其中
为模态控制力。
本文基于模态滤波技术[15]，利用最优模态控制算法实现控制仿真分析。动力学方程解耦后，每阶模态的控制利用LQR方法，其中权矩阵Qi表征了对第i阶模态的势能、动能的控制要求，Ri反映了对主动杆件的控制能量要求。Qi按下式选取：
(11)
ki，mi为相应i阶相应的模态刚度，模态质量，ai，bi为对应的权系数，通过调整权系数可以实现不同的控制要求。
3.1 仿真计算
分别在桁架节点1，2，37，38，13，14，25，26，23，24，35，36 处的X，Y，Z三个方向施加0.1 mm位移，节点11，12，47，48处的X，Y，Z方向施加-0.1 mm位移。
根据优化配置结果选取6，7，17，113号杆件作为主动杆件。节点1位移响应如图5所示。为检验优化配置的效果，选配39，95，117，146号杆件为主动杆件，取相同的控制权系数，此时节点1位移响应如图6所示，两种配置时的控制电压分别如图7，图8所示。
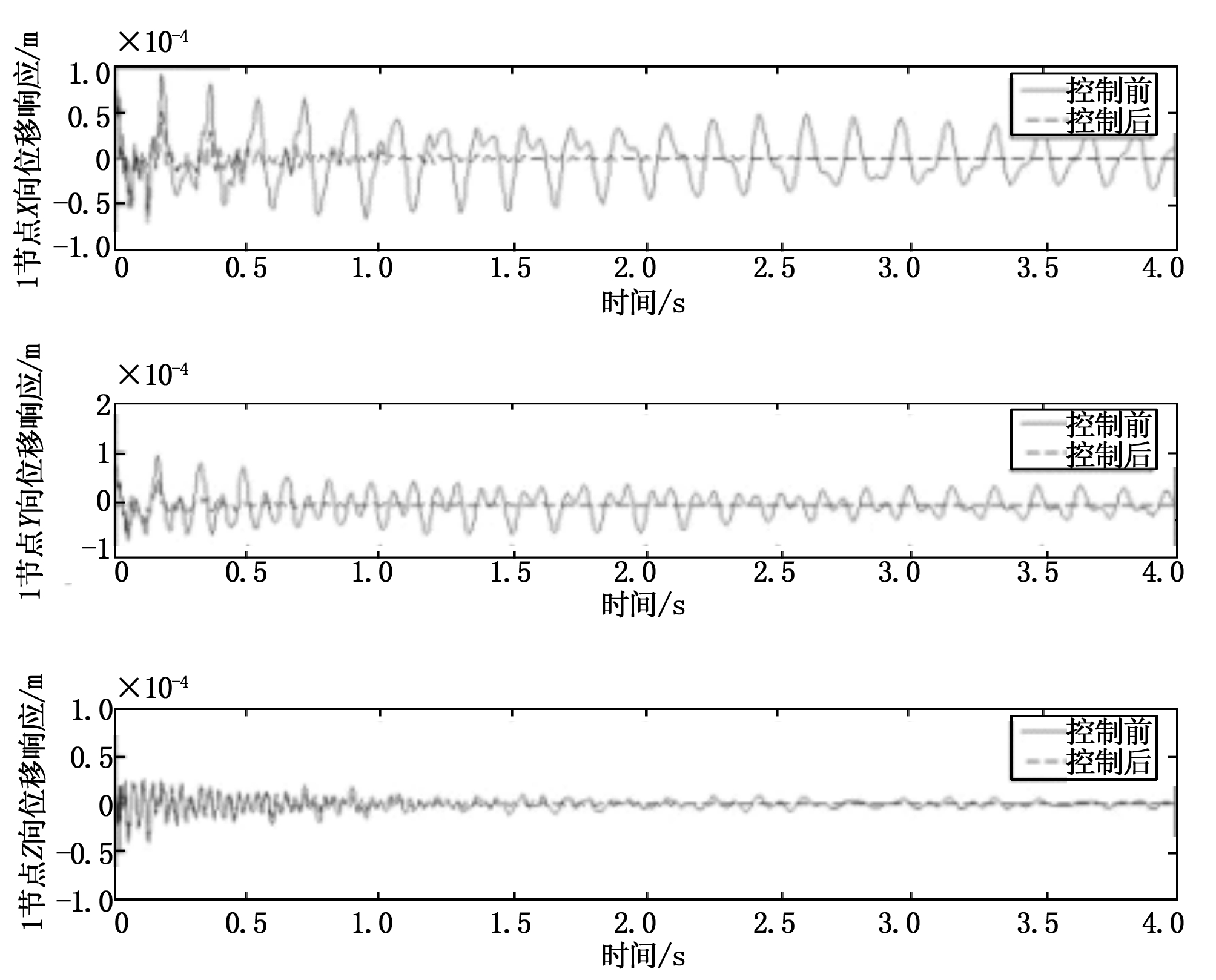
图5 优化配置时1节点位移响应
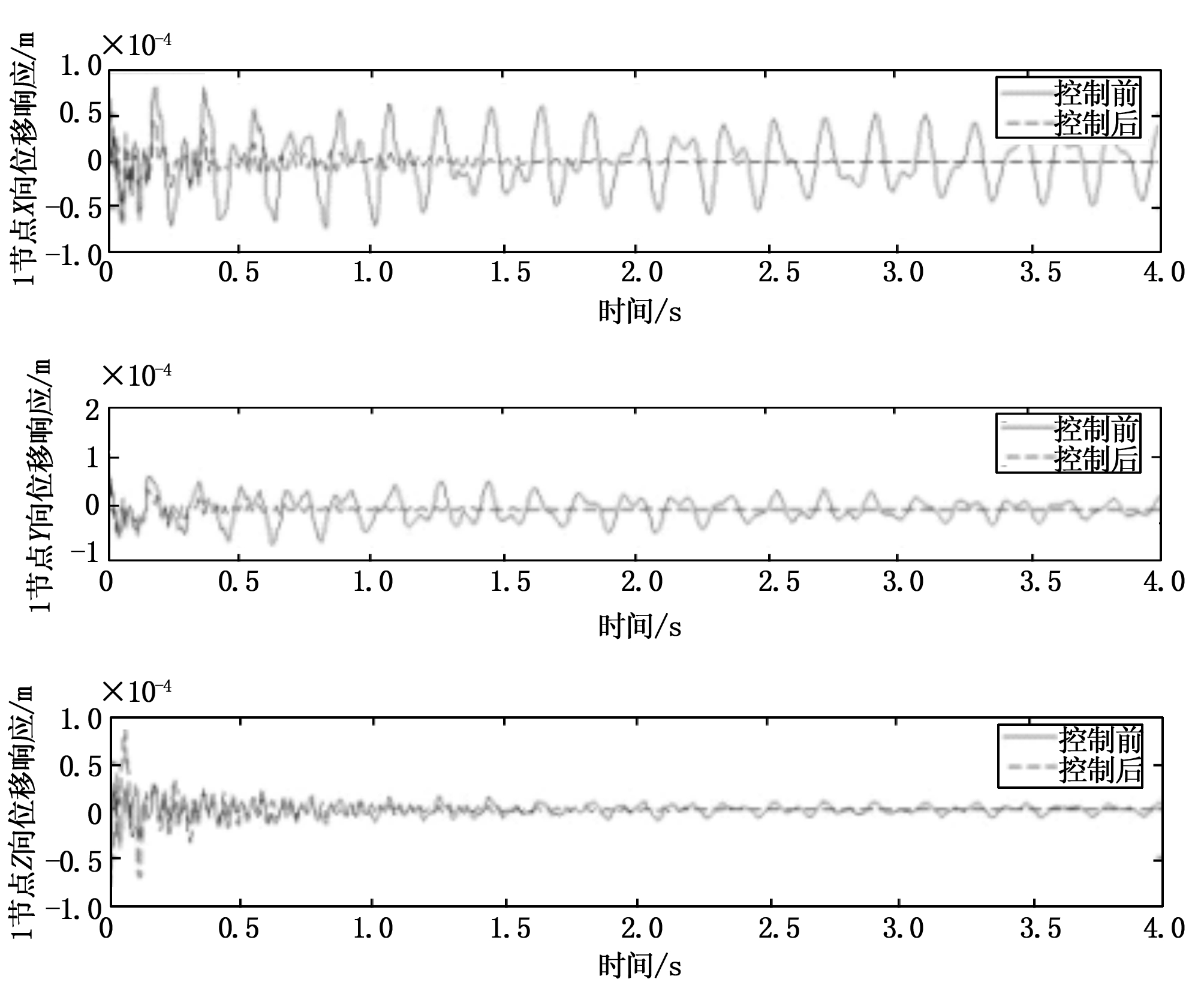
图6 选配位置时1节点位移响应
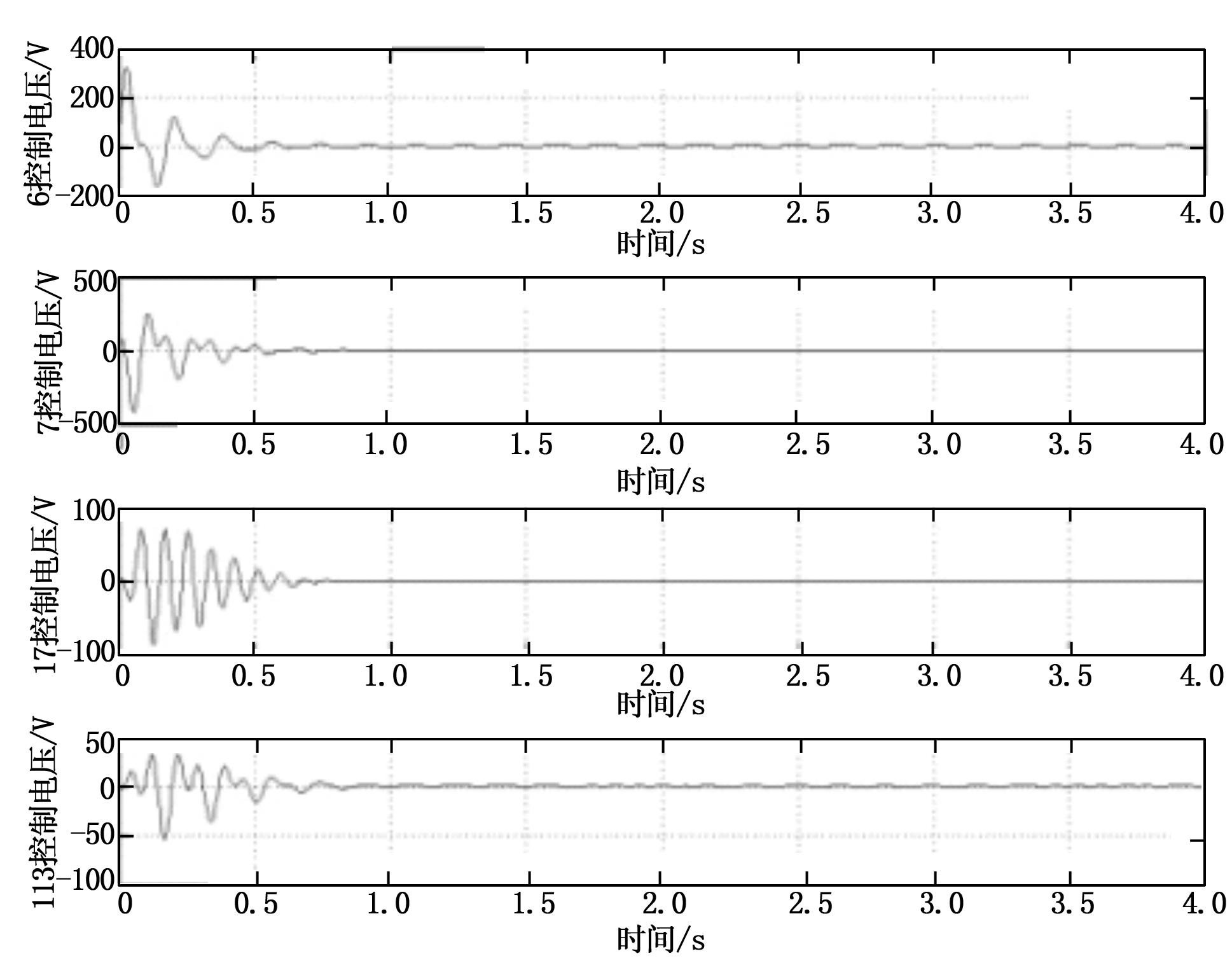
图7 优化位置控制电压
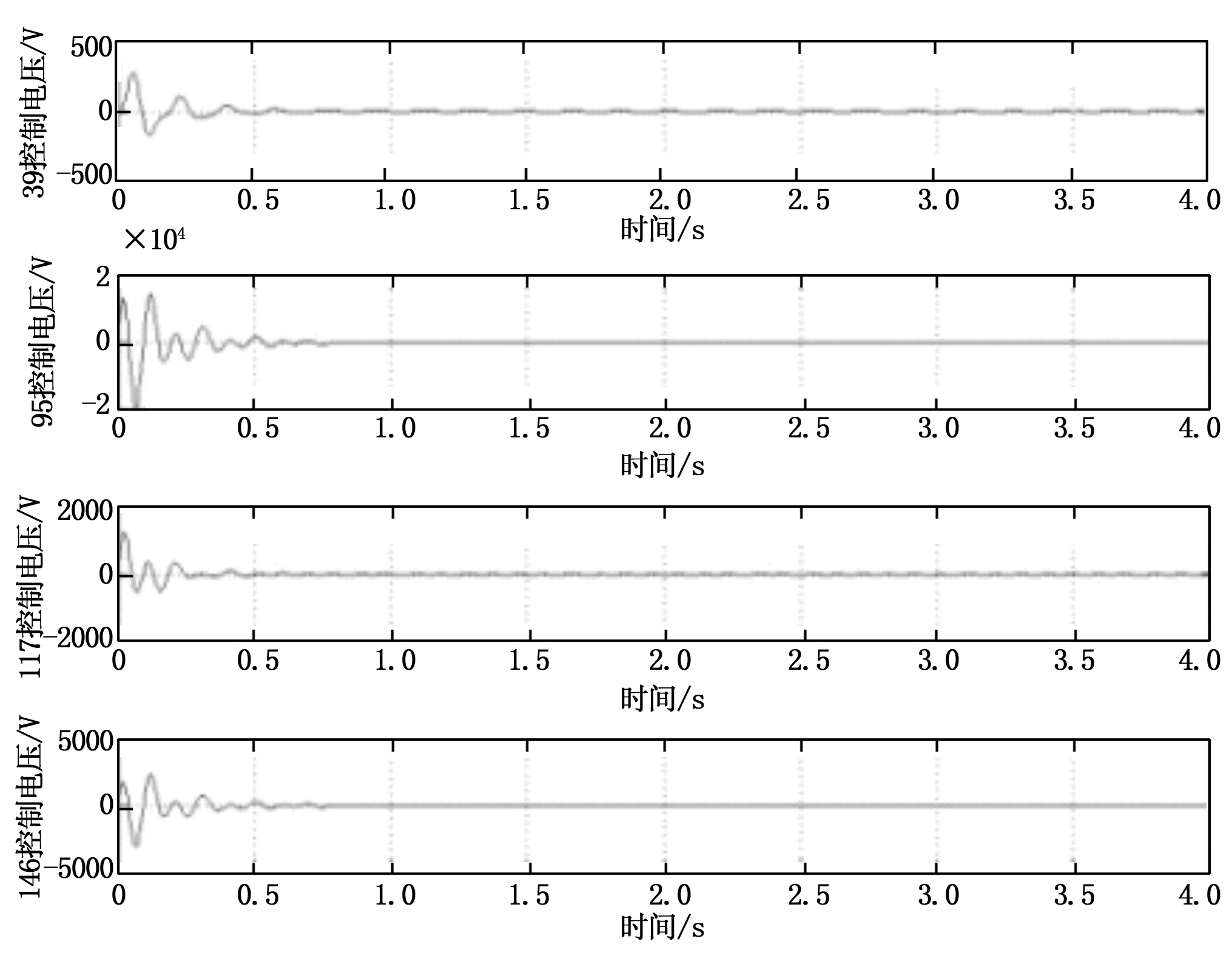
图8 选配位置控制电压
图5表明，XY向振动得到明显抑制，但Z向振动控制效果不明显，这是因为前四阶没有Z向的主振动，结构自身衰减较快。图6表明，XY向振动得到抑制，但Z向振动出现较大过调。图7表明，优化位置控制电压峰值在400 V左右，而图8表明，选配位置控制电压峰值接近20 000 V，因此优化位置控制电压分布更合理。
图5～图8结果表明，优化配置时的控制效果明显优于选配位置。
3.2 控制仿真效果评价
根据式(12)确定控制仿真过程中结构反应的峰值和均方值的评价指标：
(12)
其中:分母表示对应项的无控值，分子代表对应的有控值。|·|表示取绝对值，
表示取时域均方值，对于离散的时域值取其欧式范数值。这两个指标可以表征对位移响应峰值和最大位移响应的综合抑制效果。
仿真过程中作动器评价指标如公式(13)所示：
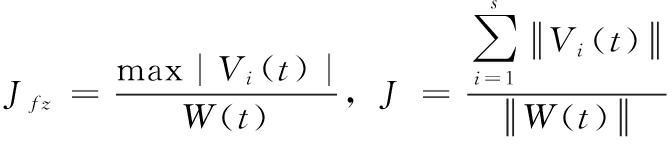
(13)
其中：s为作动器个数，W(t)=1 000 V为击穿电压。s和W(t)可表征电压峰值和控制能量。
对初始位移扰动，位移衰减时间指标具体定义为：
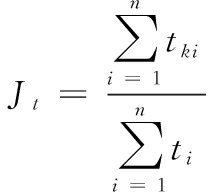
(14)
其中:tki，ti分别定义为第i节点施加控制和没有控制时位移响应衰减到结构无控时该点位移响应最大值5%所需的时间，为结构节点总数。Jt可综合评价结构振动衰减快慢。
相同初始条件或相同激励信号下，初始位移扰动的控制评价结果见表3。
按照定义的评价指标，对正弦激励，随机激励的振动控制进行验证。选配124号杆件为激励杆件，同时配置6，7，17，113号杆件作为控制杆件进行正弦激励及随机激励的控制仿真效果评价。正弦激励电压信号假定为：
随机激励电压信号为0-200 V平稳随机信号，评价结果见表4。
从表3，表4可以清楚地比较控制效果，可以发现优化位置的各项指标值明显优于非优化位置，振动抑制效果明显，控制能耗低，整体结构的振动控制效果良好。评价结果表明本文采用的杆件优化措施和控制算法对大型桁架结构的整体振动控制是非常有效的。对于其他的不同边界条件，可以按照同样的方法给出评价，也可以对不同的控制算法进行控制效果评价。
表3 初始位移扰动振动控制评价
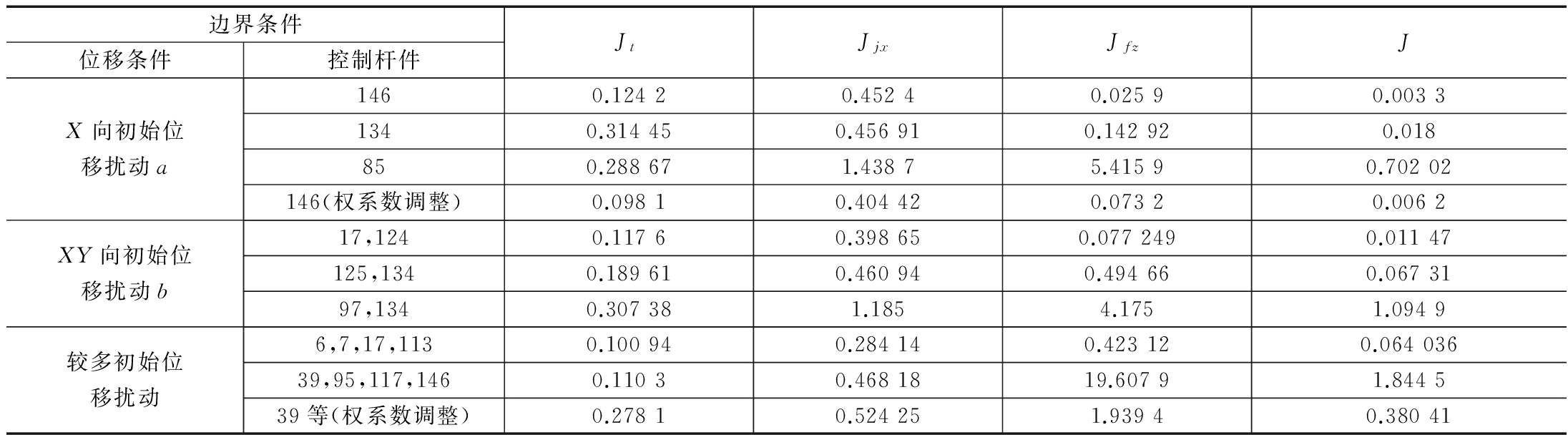
边界条件位移条件控制杆件JtJjxJfzJX向初始位移扰动a1460.12420.45240.02590.00331340.314450.456910.142920.018850.288671.43875.41590.70202146(权系数调整)0.09810.404420.07320.0062XY向初始位移扰动b17,1240.11760.398650.0772490.01147125,1340.189610.460940.494660.0673197,1340.307381.1854.1751.0949较多初始位移扰动6,7,17,1130.100940.284140.423120.06403639,95,117,1460.11030.4681819.60791.844539等(权系数调整)0.27810.524251.93940.38041
(1. X向初始位移扰动为节点1X向施加0.1 mm初始位移，节点24X向施加-0.1 mm初始位移; 2. X、Y向初始位移扰动为节点1X、Y向施加0.1 mm初始位移，节点24X、Y向施-0.1 mm初始位移)
表4 正弦、随机振动控制评价
边界条件激励形式控制杆件JfxJjxJfzJ124杆正弦激励6,7,17,1130.58800.600170.26370.302096等(权系数调整)0.297560.293870.46610.46386124杆随机激励6,7,17,1130.321880.452670.09270.054686等(权系数调整)0.225360.272950.17490.15582
4 结论
本文研究了空间柔性桁架结构的振动抑制问题，完成了结构动力学建模、主动杆件的优化配置以及振动主动控制仿真，主要结论如下：
1)建立了考虑刚性连接和弹性连接的压电杆件的机电耦合模型，并采用ANSYS、Matlab编制了空间柔性桁架结构动力学分析程序，为动力学分析和控制研究提供了方法和研究基础。
2)提出了可控性度量指标与逐步消减法相结合的优化方法，实现了空间桁架结构主动杆件的优化配置。
3)采用模态最优控制算法实现了空间桁架结构的振动控制仿真，表明优化配置的振动抑制效果优于非优化配置，并且整体结构振动控制效果良好。
